백준 1753 최단경로

https://www.acmicpc.net/problem/1753

1753번: 최단경로

📌 해결순서

다익스트라 알고리즘의 제일 기본적인 유형

 

문제를 풀기전에 다익스트라 알고리즘의 동작과정부터 생각해보자.

위의 그림과 같은 방향 그래프가 있다고 생각해보자

목표는 1번노드에서 출발해 2, 3, 4 노드로 이동하는데 드는  최소 비용을 저장하는 Distance Table 을 구하는 것이다.

탐색을 시작하기 전에 모든 노드는 방문하지 않았으므로, 거리를 INFINITY로 두고 시작한다.

1번노드에서 출발에서 출발하므로, 거리는 0 이고 방문 표시를 해준다

2, 3, 4 노드와 연결되어 있기 때문에, 각 노드로 이동하는데 드는 비용은 INFINITY 보다 작다. 따라서, 테이블 업데이트를 해준다

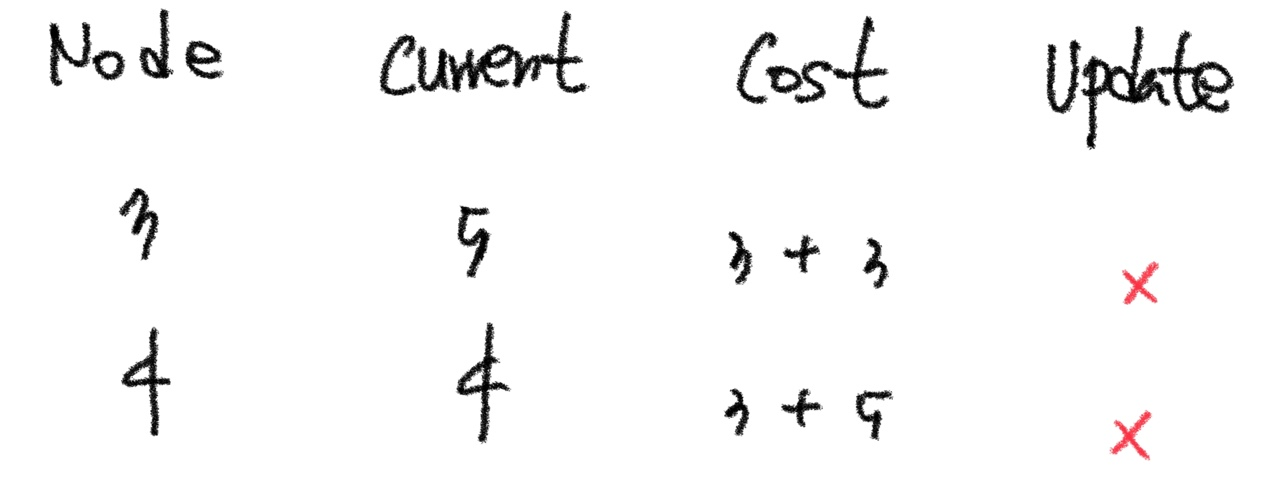
1번노드에서 목표 노드로 바로 이동하는것 보다, 다른 노드를 거쳐서 목표 노드로 이동하는 것이 더 적은 비용이 들수 있다. 따라서 모든 경우의 수에 대해서 탐색을 해야한다. 다음으로 이동 하자~

2번노드는 3, 4 와 연결되어 있다. 1번노드에서 2번 노드를 거쳐서 3, 4번 노드로 이동하는 비용에 대해서 생각해보자

1 -> 2 -> 3 = 6 >>> 1 -> 3 = 5 갱신 X

1 -> 2 -> 4 = 8 >>> 1 -> 4 = 4 갱신 X

이제 3번노드로 이동해서 반복

1 -> 3 -> 4 = 6 >>> 1 -> 4 = 4 갱신 X

모든 경로에 대해서 탐색을 완료하면, 1번 노드에서 출발해서 다른 모든 노드로 이동하는 경로의 최소가 저장된 테이블을 얻을 수 있다.

여기서 생각해 볼것은, 1번노드에서 무조건 다른 모든 노드로 이동할 수 있는것은 아니다. 그럴때는 그 노드의 테이블 값이 INFINITY로 초기상태와 같다

 

이 문제를 해결하는 과정에서, 시간복잡도를 줄이기 위해서 heap 자료구조를 사용하는데,

heap은 큐 자료구조에서 각각의 데이터에 우선순위를 부여한다는 특징이 있다.

heap 자료구조를 사용해서 오름차순을 한번 해보면 이 자료구조에 대해서 이해하기 쉽다

 

파이썬에서 배열에 하나씩 원소를 넣는 경우에, 가장 마지막에 추가한 원소가 마지막 자리에 위치한다.

heap은 각 원소에 우선순위를 부여할 수 있어서 데이터를 넣는 과정에서 정렬을 한다

import heapq

def heapSort(nums):
    h = []
    result = []

    for num in nums:
        heapq.heappush(h, -num)

    for _ in range(len(h)):
        result.append(-heapq.heappop(h))

    return result


ans = heapSort([1, 3, 5, 7, 9, 2, 4, 6, 8, 0])
print(ans)

그렇다면, 어떻게 이 문제에 heap을 활용할 수 있을까?

예를 들어서,

1 -> 3 비용이 4

1 -> 4 비용이 1 이라서 4부터 탐색을 진행하는데, 1 -> 4 -> 3 비용이 1 + 1 = 2 라면 1 -> 4 -> 3 경로에 대해서 먼저 탐색할 수 있도록 우선순위를 부여한다. 

이 과정을 heap을 사용하지 않고, 기본 list를 사용하면 시간복잡도가 O(n^2) 인데, 이유는 다음노드를 결정하기 위한 선형탐색을 O(n)번 반복하기 때문이다.

그래서 이를 해결하기 위해서, 한번 선형탐색할때 다음 노드를 결정할 수 있도록 해준다.

 

📌 코드

import sys
import heapq

input = sys.stdin.readline

INF = int(1e9)
v, e = map(int, input().split())
start = int(input())
graph = [[] for _ in range(v + 1)]
distance = [INF] * (v + 1)

for _ in range(e):
    a, b, c = map(int, input().split())
    graph[a].append((b, c))


def dijkstra(start):
    q = []
    heapq.heappush(q, (0, start))
    distance[start] = 0

    while q:
        dist, now = heapq.heappop(q)

        if distance[now] < dist:
            continue

        for i in graph[now]:
            cost = distance[now] + i[1]
            if cost < distance[i[0]]:
                distance[i[0]] = cost
                heapq.heappush(q, (cost, i[0]))


dijkstra(start)

for i in range(1, v + 1):
    if distance[i] == INF:
        print("INF")
    else:
        print(distance[i])